Skillnad mellan versioner av "4.3 10-logaritmer"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(222 mellanliggande versioner av samma användare visas inte)
Rad 2: Rad 2:
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Selected tab|[[3.4 10-logaritmer|Genomgång]]}}
+
{{Not selected tab|[[4.2 Introduktion till logaritmer: Exponentialfunktioner|  <<&nbsp;&nbsp; Förra avsnitt]]}}
−
{{Not selected tab|[[3.4 Quiz till 10-logaritmer, ver 2|Quiz]]}}
+
{{Selected tab|[[4.3 10-logaritmer|Genomgång]]}}
−
{{Not selected tab|[[3.4 Övningar till 10-logaritmer|Övningar]]}}
+
{{Not selected tab|[http://beta.mattekollen.se/#/app/section Quiz i Mattekollen]}}
−
{{Not selected tab|[[3.4 Lathund till 10-logaritmer|Lathund]]}}
+
<!-- {{Not selected tab|[[4.3 Quiz till 10-logaritmer|Quiz]]}}} -->
−
{{Not selected tab|[[3.5 Logaritmlagarna|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
+
{{Not selected tab|[[4.3 Övningar till 10-logaritmer|Övningar]]}}
 +
<!-- {{Not selected tab|[[4.3 Lathund till 10-logaritmer|Lathund]]}} -->
 +
{{Not selected tab|[[4.4 Logaritmlagarna & Logaritmer med olika baser|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
−
<big>
 
−
Logaritm är bara ett annat ord för exponent.
 
  
 +
= <b><span style="color:#931136">10-logaritmen</span></b> =
 +
<br>
 +
<table>
 +
<tr>
 +
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: 10-logaritm_390.jpg]]
 +
<br><br>
 +
<div class="ovnC">
 +
<big><b><span style="color:#931136"><math>\lg 100</math></span></b> = tal som basen <math>10</math> ska upp-
  
−
<div style="border:1px solid black;display:inline-table;margin-left: 50px;">[[Image: 10_logaritmen_Ny_600a.jpg]]</div>
+
höjas till, för att ge <math>100</math>. Det talet är <math>{\color{Red} 2}</math>.
 +
</big></div>
 +
</td>
 +
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;</td>
 +
  <td><div class="ovnC">
 +
<big><b><span style="color:#931136">Logaritm</span></b> &nbsp; = &nbsp; exponent
  
 +
<b><span style="color:#931136">10-logaritm</span></b> = exponent till basen <math> 10 </math>.
  
−
== <b><span style="color:#931136">Logaritmer till godtyckliga baser</span></b> ==
+
----
−
<br>
+
−
<div style="border:1px solid black;display:inline-table;margin-left: 50px;">[[Image: a_logaritmen_Ny_600a.jpg]]</div>
+
  
 +
<b><span style="color:#931136"><math>\lg</math></span></b> är symbolen för 10-logaritmen.
  
−
'''Om [[1.7 Logaritmlagarna|Logaritmlagarna]] se nästa avsnitt.'''
+
----
 +
 
 +
Potensform<span style="color:black">:</span> <math> \qquad\;\;\; 100 \; = \; 10\,^{\color{Red} 2} </math>
 +
 
 +
<math> \qquad\qquad\qquad\qquad\quad\;\,\, \Updownarrow </math>
 +
 
 +
Logaritmform<span style="color:black">:</span> <b><span style="color:#931136"><math> \quad \lg\,100 \; </math></span></b><math> \; = \; {\color{Red} 2} </math>
 +
</big></div>
 +
 
 +
 
 +
<div class="border-divblue">
 +
<big><b><span style="color:#931136"><math>\lg a \, </math></span></b> = &nbsp; tal som basen <math>10</math> ska upphö-
 +
 
 +
<math> \qquad\;\;\; </math> jas till, för att ge <math> \, a \, </math>.  
 +
</big></div>
 +
</td>
 +
</tr>
 +
</table>
 +
 
 +
 
 +
<big><big>
 +
<math> 10</math>-logaritmen får man genom att skriva om den kända potensformen till den ekvivalenta logaritmformen<span style="color:black">:</span>
 
</big>
 
</big>
  
 +
<math> \qquad {\rm Potensformen\quad} 10^{\,2} \, = \, 100 \qquad\quad \Longleftrightarrow \qquad\quad {\rm Logaritmformen\quad} 2 \, = \, \lg\,100 </math>
 +
</big>
  
−
== <b><span style="color:#931136">Inversegenskapen</span></b> ==
 
  
 +
= <b><span style="color:#931136">Exempel på 10-logaritmer</span></b> =
 +
<br>
 +
<table>
 +
<tr>
 +
<td>
 
<div class="ovnE">
 
<div class="ovnE">
−
==== <b><span style="color:#931136">Experiment</span></b> ====
+
<big><b><span style="color:#931136"><math>\lg 125 \, </math></span></b> = &nbsp; tal som basen <math>10</math> ska upp-
  
−
Ta fram din miniräknare och mata först in <big><div class="smallBox"> <math> 10 \, </math><span style="color:black">''^''</span> </div></big>&nbsp;&nbsp; och sedan<span style="color:black"></span> <big><math> \qquad 2,5 </math></big>
+
<math> \qquad\quad\;\;\; </math> höjas till, för att ge <math>125</math>.
  
−
Stäng parentesen och tryck på ENTER. Låt resultatet, <span style="color:red">något decimaltal</span>, stå i displayen.
+
----
  
−
Tryck på funktionsknappen för <math> \, 10</math>-logaritmen:
+
Räknaren<span style="color:black">:</span> <small><math> \boxed{\text{LOG}}</math></small> <math>(125) = </math> <small><math> {\color{Red} {2,09691\ldots}} </math></small>
  
−
::::::::::<div class="smallBox"> <math> {\rm{LOG}} </math> </div>
+
----
  
−
Tryck på ANS (ANSwer lagrar räknarens sist beräknade värde), i vårt fall <span style="color:red">decimaltalet ovan</span>.
+
Potensform<span style="color:black">:</span> <math> \;\;\; 125 \; = \; 10\,^{\color{Red} {2,09691\ldots}} </math>
  
−
Stäng parentesen och tryck på ENTER: Du får tillbaka <math> \, 2,5 \, </math> som du hade matat in i början.
+
<math> \qquad\qquad\qquad\quad\;\,\, \Updownarrow </math>
  
−
Experimentet har visat:
+
Log-form<span style="color:black">:</span> <b><span style="color:#931136"><math> \;\; \lg\,125 \; </math></span></b><math> \; = \; {\color{Red} {2,09691\ldots}} </math>
 +
</big></div>
 +
</td>
 +
<td> <math> \qquad </math> </td>
 +
<td><div class="ovnE">
 +
<big><b><span style="color:#931136"><math>\lg 45 \, </math></span></b> = &nbsp; tal som basen <math>10</math> ska upp-
  
−
::::::::<big><math> \lg\,(10^{\,2,5}) \, = \, 2,5 </math></big>
+
<math> \qquad\quad\; </math> höjas till, för att ge <math>45</math>.
−
</div>
+
  
 +
----
 +
 +
Räknaren<span style="color:black">:</span> <small><math> \boxed{\text{LOG}}</math></small> <math>(45) = </math> <small><math> {\color{Red} {1,65321\ldots}} </math></small>
 +
 +
----
 +
 +
Potensform<span style="color:black">:</span> <math> \;\;\;\;\; 45 \; = \; 10\,^{\color{Red} {1,65321\ldots}} </math>
 +
 +
<math> \qquad\qquad\qquad\quad\;\,\, \Updownarrow </math>
 +
 +
Log-form<span style="color:black">:</span> <b><span style="color:#931136"><math> \;\;\;\; \lg\,45 \; </math></span></b><math> \; = \; {\color{Red} {1,65321\ldots}} </math>
 +
</big></div>
 +
</td>
 +
</tr>
 +
</table>
 +
 +
 +
<big> I räknaren står knappen <math> \; \boxed{\rm{LOG}} \; </math> för <math> \, 10</math>-logaritmen, medan man använder symbolen <big><math> \lg \, </math></big> när man skriver.  </big>
 +
 +
 +
<div class="ovnC">
 +
<big><b><span style="color:#931136"><math>\lg\,0,1</math></span></b> = <math>\lg\,(\frac{1}{10})</math> = tal som basen <math>10</math>
 +
 +
ska upphöjas till, för att ge <math>\frac{1}{10}</math>.
 +
 +
----
 +
 +
Potensform<span style="color:black">:</span> <math> \quad\;\;\; \frac{1}{10} \; = \; 10\,^{\color{Red} {-1}} </math>
 +
 +
<math> \qquad\qquad\qquad\qquad\, \Updownarrow </math>
 +
 +
Log-form<span style="color:black">:</span> <b><span style="color:#931136"><math> \;\;\;\; \lg\,0,1 \; </math></span></b><math> \; = \; {\color{Red} {-1}} </math>
 +
</big></div>
 +
 +
 +
= <b><span style="color:#931136">10-logaritmfunktionen och dess definitionsmängd</span></b> =
 +
<br>
 +
<table>
 +
<tr>
 +
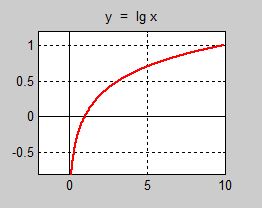
<td> [[Image: lga.jpg]] <br><br> &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<big><b><span style="color:red">10-logaritmfunktionen</span></b></big></td>
 +
<td> <math> \qquad </math> </td>
 +
<td>
 +
<div class="border-divblue">
 
<big>
 
<big>
−
Experimentet ovan är ett exempel på att <small><div class="smallBox"><math>{\rm{LOG}} \, </math> </div></small> &nbsp; är den inversa operationen till <small><div class="smallBox"><math>10 \, </math><span style="color:black">''^''</span> </div></small>&nbsp; . Generellt gäller:
+
Funktionen <b><span style="color:#931136"><math> \, y \, = \, \lg x \, </math></span></b> är definierad endast
  
 +
för <math> \, x>0 \, </math>. För <math> \, x \leq 0 \, </math> är den <b><span style="color:red">inte</span></b> definierad.
 +
 +
Exempel:
 +
<small>
 +
<div class="ovnE">
 +
<small>
 +
<math> \boxed{\text{LOG}}</math> <math>({\color{Red} {-1}}) \quad \rightarrow \quad {\color{Red} {\text{ERROR}}} </math>
 +
 +
<math> \boxed{\text{LOG}}</math> <math>({\color{Red} {\;0\;}}) \quad\, \rightarrow \quad {\color{Red} {\text{ERROR}}} </math>
 +
</small></div>
 +
</small>
 +
</big></div>
 +
 +
 +
</td>
 +
</tr>
 +
</table>
 +
<big>Definitionsmängden ovan gäller endast inom de reella talen.
 +
 +
För <math> \, x < 0 \, </math> har <math> \, y \, = \, \lg x \, </math> komplexa värden.
 +
 +
Här behandlas 10-logaritmen endast inom de reella talen.</big>
 +
 +
 +
= <b><span style="color:#931136">Inversegenskapen</span></b> =
 +
<br>
 +
<big>Ta fram din miniräknare och genomför följande två experiment:</big>
 +
 +
 +
<div class="ovnE">
 +
==== <b><span style="color:#931136">Experiment 1</span></b> ====
 +
 +
Tryck på knappen för <math> \, 10</math>-logaritmen <math> \quad \boxed{\text{LOG}} \quad </math> &nbsp;&nbsp; och mata in sedan<span style="color:black"></span> <math> \qquad {\color{Red} {1,5}} </math>
 +
 +
Stäng parentesen och tryck på ENTER. Låt resultatet, <span style="color:blue">något decimaltal</span>, stå i displayen.
 +
 +
Mata in nu <math> 10 </math> <math> \boxed{\text{ ^ }} </math> och tryck sedan på knappen <span style="color:blue"><math> \; \boxed{\text{ANS}} \; </math></span> som lagrar <span style="color:blue">decimaltalet</span> ovan.
 +
 +
Stäng parentesen och tryck på ENTER: Du får tillbaka <math> \, {\color{Red} {1,5}} \, </math> som du matat in i början.
 +
 +
Experiment 1 har visat:
 +
 +
:::::::::<big><math> 10^{\,\lg{\color{Red} {1,5}}} \, = \, {\color{Red} {1,5}} </math></big>
 +
</div>
 +
<br>
 +
<div class="ovnC">
 +
 +
==== <b><span style="color:#931136">Experiment 2</span></b> ====
 +
 +
Mata in först &nbsp; <math> 10 </math> <math> \boxed{\text{ ^ }} </math> &nbsp;&nbsp; och sedan<span style="color:black"></span> <math> \qquad {\color{Red} {2,5}} </math>
 +
<!-- <big><div class="smallBox"> <math> 10 \, </math><span style="color:black">''^''</span> </div></big> -->
 +
 +
Stäng parentesen och tryck på ENTER. Låt resultatet, <span style="color:blue">något decimaltal</span>, stå i displayen.
 +
 +
Tryck på knappen för <math> \, 10</math>-logaritmen <math> \quad \boxed{\text{LOG}} \quad </math> och sedan på knappen <span style="color:blue"><math> \quad \boxed{\text{ANS}} \quad </math></span>.
 +
 +
Stäng parentesen och tryck på ENTER: Du får tillbaka <math> \, {\color{Red} {2,5}} \, </math> som du matat in i början.
 +
 +
Experiment 2 har visat:
 +
 +
:::::::::<big><math> \lg\,(10^{\,{\color{Red} {2,5}}}) \, = \, {\color{Red} {2,5}} </math></big>
 +
</div>
 +
 +
 +
<big>
 +
Generellt gäller:
  
 
<div class="border-divblue">
 
<div class="border-divblue">
 
<math> 10</math>-logaritmen <math> \, y \, = \, \lg\,x \, </math> är den <b><span style="color:red">inversa</span></b> (motsatta) funktionen till exponentialfunktionen <math> \, y \, = \, 10\,^x \, </math>, dvs<span style="color:black">:</span>
 
<math> 10</math>-logaritmen <math> \, y \, = \, \lg\,x \, </math> är den <b><span style="color:red">inversa</span></b> (motsatta) funktionen till exponentialfunktionen <math> \, y \, = \, 10\,^x \, </math>, dvs<span style="color:black">:</span>
  
−
::<math> \lg\,(10^{\,x}) \, = \, x \qquad {\rm och\; } \qquad 10^{\,\lg\,x} \, = \, x \qquad\quad {\rm I\;ord:\quad } 10^{\,x} {\rm \;och\; } \lg\,x \;{\rm {\color {Red} {tar\;ut\;varandra}}.} </math>
+
<math> \qquad \lg\,(10^{\,{\color{Red} x}}) \, = \, {\color{Red} x} \quad {\rm och\; } \quad 10^{\,\lg{\color{Red} x}} \, = \, {\color{Red} x} \qquad\quad </math> I ord<span style="color:black">:</span> <small><math> \quad \boxed{\text{LOG}} \; </math></small> &nbsp; och &nbsp; <math> \; 10 </math> <small><math> \boxed{\text{ ^ }} \; </math></small> &nbsp; <b><span style="color:red">tar ut varandra</span></b>&nbsp;.
 
</div>
 
</div>
  
Rad 64: Rad 217:
 
Både <math> \lg\,(10^{\,x}) </math> och <math> 10^{\,\lg\,x} </math> är exempel på s.k. <b><span style="color:red">sammansatta funktioner</span></b>. För sådana funktioner gäller regeln:
 
Både <math> \lg\,(10^{\,x}) </math> och <math> 10^{\,\lg\,x} </math> är exempel på s.k. <b><span style="color:red">sammansatta funktioner</span></b>. För sådana funktioner gäller regeln:
  
−
Sammansatta funktioner beräknas <b><span style="color:red">inifrån</span></b>: Experimentet ovan var ett exempel på detta. För att få <math> \, \lg\,(10^{\,2,5}) \, </math>, beräknades först <math> \, 10^{\,2,5} </math> och sedan <math> \, \lg\,(10^{\,2,5}) </math>.
+
Sammansatta funktioner beräknas <b><span style="color:red">inifrån</span></b>: Experimenten ovan var exempel på detta. För att t.ex. få <math> \, \lg\,(10^{\,2,5}) \, </math>, beräknades först <math> \, 10^{\,2,5} </math> och sedan <math> \, \lg\,(10^{\,2,5}) </math>.
 
</big>
 
</big>
  
  
−
<div class="ovnE">
+
= <b><span style="color:#931136">Exponentialekvationer av typ <math> \; 10\,^x \, = \, b \; </math></span></b> =
−
<big><b><span style="color:#931136">Exempel på inversegenskapen</span></b></big>
+
  
 +
<div class="ovnE">
 +
Logaritmering och användning av inversegenkapen löser denna typ av ekvation:
 
<div class="exempel">
 
<div class="exempel">
 
<math>\begin{array}{rcll}
 
<math>\begin{array}{rcll}
−
{\rm {\color{Red} {Potensformen:}}\qquad\quad}           10^{\,x} & = & 68                &  {\rm Logaritmera\;båda\;leden\;med\;\lg} \\
+
{\rm Potensform:\qquad\qquad}         10^{\,x} & = & 68                &  {\rm Logaritmera\;båda\;leden\;med\;\lg}                     \\
−
                        \lg\,(10^{\,x}) & = & \lg\,68          &  {\rm Använd\;inversegenskapen\;på\;VL}   \\
+
{\color{Red} {\lg}}\,({\color{Red} {10}}^{\,x}) & = & \lg\,68          &  {\color{Red} {\lg}} {\rm \;och\;} {\color{Red} {10}}^{\,\cdot} {\rm \;tar\;ut\;varandra\;i\;VL} \\
−
{\rm {\color{Red} {Logaritmformen:}}\qquad\quad}                 x & = & \lg\,68          &                                           \\
+
{\rm Logaritmform:\qquad\qquad}               x & = & \lg\,68          &                                                               \\
−
                                      x & = & 1,832508913\ldots &                                           \\
+
                                              x & = & 1,832508913\ldots &                                                               \\
−
{\rm Kontroll:\qquad} 10^{\,1,832508913} & = & 68                &   
+
{\rm Kontroll:\qquad}       10^{\,1,832508913} & = & 68                &   
 
         \end{array}</math>
 
         \end{array}</math>
−
</div></div>
+
</div>
 +
Att lösa ekvationen <math> \, 10\,^x = b \, </math> innebär att skriva om den från potensformen till logaritmform, dvs<span style="color:black">:</span>
 +
 
 +
<math> \qquad {\rm Potensformen\quad} 10^{\,x} \, = \, b \qquad\quad \Longleftrightarrow \qquad\quad {\rm Logaritmformen\quad} x \, = \, \lg\,b </math>
 +
 
 +
Inversegenkapen tillåter övergången i båda riktningar genom logaritmering resp. exponentiering.
 +
</div>
 +
 
 +
 
 +
<big>Generellt:</big>
 +
 
 +
<div class="border-divblue">
 +
<big>Exponentialekvationen <math> \;\;\; 10\,^x \, = \, b </math>
 +
 
 +
har lösningen<span style="color:black">:</span> <math> \qquad\qquad\quad x \, = \, \lg\,b </math>
 +
</big></div>
  
  
Rad 104: Rad 273:
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2017 Taifun Alishenas. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2023 <b><span style="color:blue">Lieta AB</span></b>. All Rights Reserved.

Nuvarande version från 30 april 2024 kl. 11.08

        <<   Förra avsnitt          Genomgång          Quiz i Mattekollen          Övningar          Nästa avsnitt  >>      


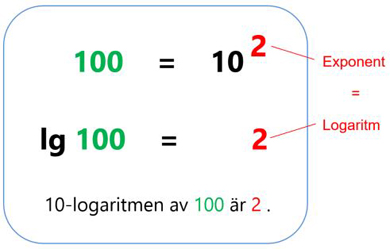
10-logaritmen


              10-logaritm 390.jpg



\(\lg 100\) = tal som basen \(10\) ska upp-

höjas till, för att ge \(100\). Det talet är \({\color{Red} 2}\).

          

Logaritm   =   exponent

10-logaritm = exponent till basen \( 10 \).

\(\lg\) är symbolen för 10-logaritmen.

Potensform: \( \qquad\;\;\; 100 \; = \; 10\,^{\color{Red} 2} \)

\( \qquad\qquad\qquad\qquad\quad\;\,\, \Updownarrow \)

Logaritmform: \( \quad \lg\,100 \; \)\( \; = \; {\color{Red} 2} \)


\(\lg a \, \) =   tal som basen \(10\) ska upphö-

\( \qquad\;\;\; \) jas till, för att ge \( \, a \, \).


\( 10\)-logaritmen får man genom att skriva om den kända potensformen till den ekvivalenta logaritmformen:

\( \qquad {\rm Potensformen\quad} 10^{\,2} \, = \, 100 \qquad\quad \Longleftrightarrow \qquad\quad {\rm Logaritmformen\quad} 2 \, = \, \lg\,100 \)


Exempel på 10-logaritmer


\(\lg 125 \, \) =   tal som basen \(10\) ska upp-

\( \qquad\quad\;\;\; \) höjas till, för att ge \(125\).

Räknaren: \( \boxed{\text{LOG}}\) \((125) = \) \( {\color{Red} {2,09691\ldots}} \)

Potensform: \( \;\;\; 125 \; = \; 10\,^{\color{Red} {2,09691\ldots}} \)

\( \qquad\qquad\qquad\quad\;\,\, \Updownarrow \)

Log-form: \( \;\; \lg\,125 \; \)\( \; = \; {\color{Red} {2,09691\ldots}} \)

\( \qquad \)

\(\lg 45 \, \) =   tal som basen \(10\) ska upp-

\( \qquad\quad\; \) höjas till, för att ge \(45\).

Räknaren: \( \boxed{\text{LOG}}\) \((45) = \) \( {\color{Red} {1,65321\ldots}} \)

Potensform: \( \;\;\;\;\; 45 \; = \; 10\,^{\color{Red} {1,65321\ldots}} \)

\( \qquad\qquad\qquad\quad\;\,\, \Updownarrow \)

Log-form: \( \;\;\;\; \lg\,45 \; \)\( \; = \; {\color{Red} {1,65321\ldots}} \)


I räknaren står knappen \( \; \boxed{\rm{LOG}} \; \) för \( \, 10\)-logaritmen, medan man använder symbolen \( \lg \, \) när man skriver.


\(\lg\,0,1\) = \(\lg\,(\frac{1}{10})\) = tal som basen \(10\)

ska upphöjas till, för att ge \(\frac{1}{10}\).

Potensform: \( \quad\;\;\; \frac{1}{10} \; = \; 10\,^{\color{Red} {-1}} \)

\( \qquad\qquad\qquad\qquad\, \Updownarrow \)

Log-form: \( \;\;\;\; \lg\,0,1 \; \)\( \; = \; {\color{Red} {-1}} \)


10-logaritmfunktionen och dess definitionsmängd


Lga.jpg

            10-logaritmfunktionen		 \( \qquad \)

Funktionen \( \, y \, = \, \lg x \, \) är definierad endast

för \( \, x>0 \, \). För \( \, x \leq 0 \, \) är den inte definierad.

Exempel:

\( \boxed{\text{LOG}}\) \(({\color{Red} {-1}}) \quad \rightarrow \quad {\color{Red} {\text{ERROR}}} \)

\( \boxed{\text{LOG}}\) \(({\color{Red} {\;0\;}}) \quad\, \rightarrow \quad {\color{Red} {\text{ERROR}}} \)


Definitionsmängden ovan gäller endast inom de reella talen.

För \( \, x < 0 \, \) har \( \, y \, = \, \lg x \, \) komplexa värden.

Här behandlas 10-logaritmen endast inom de reella talen.


Inversegenskapen


Ta fram din miniräknare och genomför följande två experiment:


Experiment 1

Tryck på knappen för \( \, 10\)-logaritmen \( \quad \boxed{\text{LOG}} \quad \)    och mata in sedan \( \qquad {\color{Red} {1,5}} \)

Stäng parentesen och tryck på ENTER. Låt resultatet, något decimaltal, stå i displayen.

Mata in nu \( 10 \) \( \boxed{\text{ ^ }} \) och tryck sedan på knappen \( \; \boxed{\text{ANS}} \; \) som lagrar decimaltalet ovan.

Stäng parentesen och tryck på ENTER: Du får tillbaka \( \, {\color{Red} {1,5}} \, \) som du matat in i början.

Experiment 1 har visat:

\( 10^{\,\lg{\color{Red} {1,5}}} \, = \, {\color{Red} {1,5}} \)


Experiment 2

Mata in först   \( 10 \) \( \boxed{\text{ ^ }} \)    och sedan \( \qquad {\color{Red} {2,5}} \)

Stäng parentesen och tryck på ENTER. Låt resultatet, något decimaltal, stå i displayen.

Tryck på knappen för \( \, 10\)-logaritmen \( \quad \boxed{\text{LOG}} \quad \) och sedan på knappen \( \quad \boxed{\text{ANS}} \quad \).

Stäng parentesen och tryck på ENTER: Du får tillbaka \( \, {\color{Red} {2,5}} \, \) som du matat in i början.

Experiment 2 har visat:

\( \lg\,(10^{\,{\color{Red} {2,5}}}) \, = \, {\color{Red} {2,5}} \)


Generellt gäller:

\( 10\)-logaritmen \( \, y \, = \, \lg\,x \, \) är den inversa (motsatta) funktionen till exponentialfunktionen \( \, y \, = \, 10\,^x \, \), dvs:

\( \qquad \lg\,(10^{\,{\color{Red} x}}) \, = \, {\color{Red} x} \quad {\rm och\; } \quad 10^{\,\lg{\color{Red} x}} \, = \, {\color{Red} x} \qquad\quad \) I ord: \( \quad \boxed{\text{LOG}} \; \)   och   \( \; 10 \) \( \boxed{\text{ ^ }} \; \)   tar ut varandra .

Inversegenskapen gäller oberoende av operationernas ordning: Vare sig du tar först \( 10^{\,x} \) och sedan \( \lg\,x \) eller tvärt om, resultatet blir alltid \( \,x \).

Dvs man återvänder till det värde \( \,x \) man hade börjat att använda någon av dessa operationer på. Förutsättningen är förstås att man utför \( 10^{\,x} \) och \( \lg\,x \) direkt efter varandra.

Både \( \lg\,(10^{\,x}) \) och \( 10^{\,\lg\,x} \) är exempel på s.k. sammansatta funktioner. För sådana funktioner gäller regeln:

Sammansatta funktioner beräknas inifrån: Experimenten ovan var exempel på detta. För att t.ex. få \( \, \lg\,(10^{\,2,5}) \, \), beräknades först \( \, 10^{\,2,5} \) och sedan \( \, \lg\,(10^{\,2,5}) \).


Exponentialekvationer av typ \( \; 10\,^x \, = \, b \; \)

Logaritmering och användning av inversegenkapen löser denna typ av ekvation:

\(\begin{array}{rcll} {\rm Potensform:\qquad\qquad} 10^{\,x} & = & 68 & {\rm Logaritmera\;båda\;leden\;med\;\lg} \\ {\color{Red} {\lg}}\,({\color{Red} {10}}^{\,x}) & = & \lg\,68 & {\color{Red} {\lg}} {\rm \;och\;} {\color{Red} {10}}^{\,\cdot} {\rm \;tar\;ut\;varandra\;i\;VL} \\ {\rm Logaritmform:\qquad\qquad} x & = & \lg\,68 & \\ x & = & 1,832508913\ldots & \\ {\rm Kontroll:\qquad} 10^{\,1,832508913} & = & 68 & \end{array}\)

Att lösa ekvationen \( \, 10\,^x = b \, \) innebär att skriva om den från potensformen till logaritmform, dvs:

\( \qquad {\rm Potensformen\quad} 10^{\,x} \, = \, b \qquad\quad \Longleftrightarrow \qquad\quad {\rm Logaritmformen\quad} x \, = \, \lg\,b \)

Inversegenkapen tillåter övergången i båda riktningar genom logaritmering resp. exponentiering.


Generellt:

Exponentialekvationen \( \;\;\; 10\,^x \, = \, b \)

har lösningen: \( \qquad\qquad\quad x \, = \, \lg\,b \)





Internetlänkar

http://www.youtube.com/watch?v=rYHdUrKqxaU

http://goto.glocalnet.net/larsthomee/logaritm.html

http://www.kck.amal.se/webtutor/ovel/mattec/Funktioner/F3.html

http://wiki.math.se/wikis/sf0600_0701/index.php/3.3_Logaritmer





Copyright © 2023 Lieta AB. All Rights Reserved.

Hämtad från "https://kurser.mathonline.se/index.php?title=4.3_10-logaritmer&oldid=14014"