Skillnad mellan versioner av "1.3 Parallella och vinkelräta linjer"
Från Mathonline
Taifun (Diskussion | bidrag) (Skapade sidan med '__NOTOC__ {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | style="border-bottom:1px solid #797979" width="5px" | {{Not selected tab|1.2 Formel...') |
Taifun (Diskussion | bidrag) m |
||
| (8 mellanliggande versioner av samma användare visas inte) | |||
| Rad 12: | Rad 12: | ||
<div class="ovnE"> | <div class="ovnE"> | ||
| − | == <b><span style="color:#931136">Har man | + | == <b><span style="color:#931136">Har man ekvationen till en rät linje, kan ekvationen till den <span style="color:red">parallella</span> och </span></b> == |
| − | == <b><span style="color:#931136"> | + | == <b><span style="color:#931136">den <span style="color:red">vinkelrätta</span> linjen genom en viss punkt bestämmas.</span></b> == |
| − | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: | + | |
| + | |||
| + | == <b><span style="color:#931136">En formel för <span style="color:red">lutningen till vinkelräta linjer</span> kan användas.</span></b> == | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 1 3 Parallella vinkelrata linjer 800.jpg]] | ||
</div> | </div> | ||
</div> | </div> | ||
Nuvarande version från 20 mars 2024 kl. 14.35
| << Förra avsnitt | Genomgång | Övningar | Innehållsförteckning | Nästa avsnitt >> |
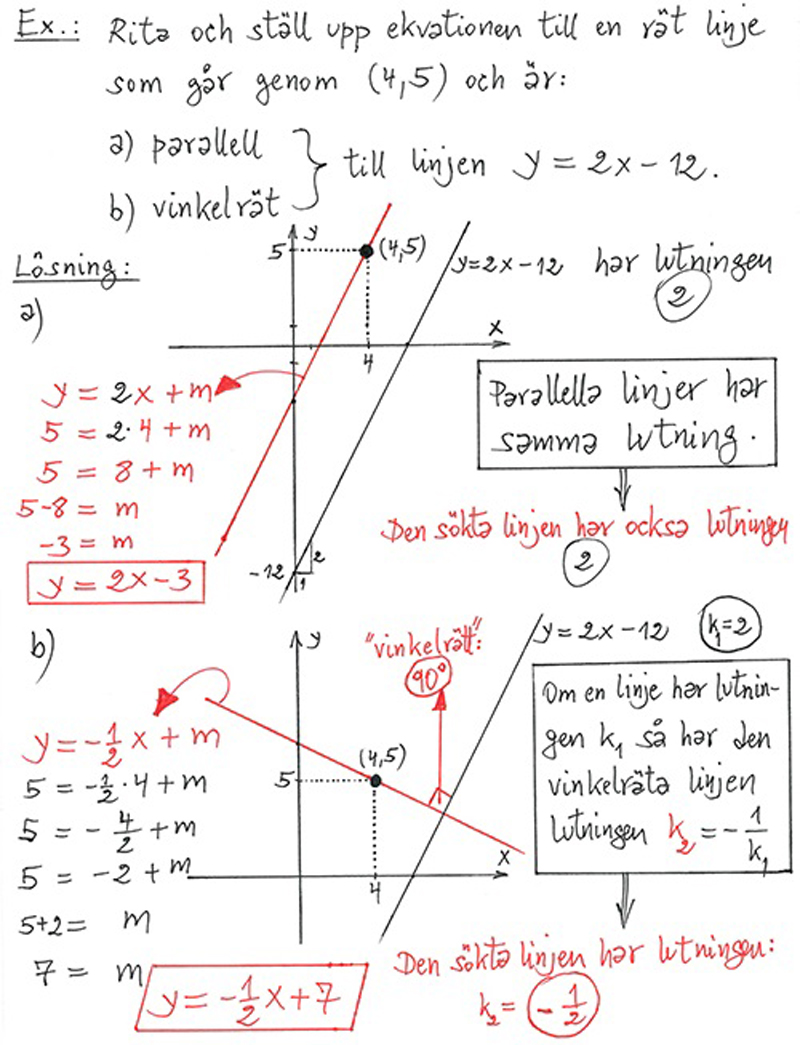
Har man ekvationen till en rät linje, kan ekvationen till den parallella och
den vinkelrätta linjen genom en viss punkt bestämmas.
En formel för lutningen till vinkelräta linjer kan användas.
Copyright © 2024 Lieta AB. All Rights Reserved.