Skillnad mellan versioner av "5.8 Lösning till Cirkel-kvadrat problemet"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (En mellanliggande version av samma användare visas inte) | |||
| Rad 4: | Rad 4: | ||
{{Not selected tab|[[5.7 Avstånds- & mittpunktsformeln|<<< Förra avsnitt]]}} | {{Not selected tab|[[5.7 Avstånds- & mittpunktsformeln|<<< Förra avsnitt]]}} | ||
{{Not selected tab|[[5.8 Problemlösning: Cirkel-kvadrat problemet|Genomgång]]}} | {{Not selected tab|[[5.8 Problemlösning: Cirkel-kvadrat problemet|Genomgång]]}} | ||
| − | {{Not selected tab|[[5.8 Övningar till | + | {{Not selected tab|[[5.8 Övningar till Problemlösning|Övningar]]}} |
{{Selected tab|[[5.8 Lösning till Cirkel-kvadrat problemet|Lösning]]}} | {{Selected tab|[[5.8 Lösning till Cirkel-kvadrat problemet|Lösning]]}} | ||
| + | {{Not selected tab|[[6.1 Statistiska observationer och lägesmått|Nästa avsnitt >> ]]}} | ||
<!-- {{Not selected tab|[[Det duala Cirkel-kvadrat problemet|Det duala problemet]]}} --> | <!-- {{Not selected tab|[[Det duala Cirkel-kvadrat problemet|Det duala problemet]]}} --> | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
Nuvarande version från 19 april 2024 kl. 08.32
| <<< Förra avsnitt | Genomgång | Övningar | Lösning | Nästa avsnitt >> |
Lösning i tre streg till dagens uppgift
Steg 1 Ta exemplet \( \, r = 4 \, \). Beräkna \( \, a = f(4) \, \). Beräkna båda figurernas areor. Vilken är större?
\( \quad\; \color{Red}{r = 4} \; \) insatt i \( \quad \)- Med \( \, r = 4 \, \) och \( \, a = 6,28 \, \) beräknar vi figurernas areor:
\( \quad\; \displaystyle A_{cirkel} \, = \, \pi \cdot r^2 \, = \, \pi \cdot 4^2 \, = \, \pi \cdot 16 \, \approx \, 3,14 \cdot 16 \, = \, \underline{50,24} \)
\( \quad\; \displaystyle A_{kvadrat} \, = \, a^2 \, = \, 6,28^2 \, = \, \underline{39,44} \).
- Slutsats: \( \quad \) Cirkelns area är större än kvadratens.
Steg 2 Ta flera exempel, t.ex. \( r = 2 \), \( \; r = 6 \; \) och \( \; r = 8 \). Gör samma sak som i steg 1.
\( \quad\; \color{Red}{r = 2} \; \) insatt i inramad formel i steg 1 ovan ger \( \quad \displaystyle a = f(2) = \frac{\pi}{2} \cdot \, 2 = \frac{\pi\cdot 2}{2} = \pi \, \approx \, 3,14 \quad \)
- Med \( \, r = 2 \, \) och \( \, a = 3,14 \, \) beräknar vi figurernas areor:
\( \quad\; \displaystyle A_{cirkel} \, = \, \pi \cdot r^2 \, = \, \pi \cdot 2^2 \, = \, \pi \cdot 4 \, \approx \, 3,14 \cdot 4 \, = \, \underline{12,56} \)
\( \quad\; \displaystyle A_{kvadrat} \, = \, a^2 \, = \, 3,14^2 \, = \, \underline{9,86} \).
- Slutsats: \( \quad \) Cirkelns area är större än kvadratens.
- Med exemplen \( \; \color{Red}{r = 6} \; \) och \( \; \color{Red}{r = 8} \; \) gör man på exakt samma sätt som med \( \, \color{Red}{r = 4} \, \) och \( \, \color{Red}{r = 2} \; \)ovan.
- Slutsatsen blir alltid: \( \quad \) Cirkelns area är större än kvadratens. \( \quad \) Frågan: Är det alltid så? \( \; \) Se steg 3.
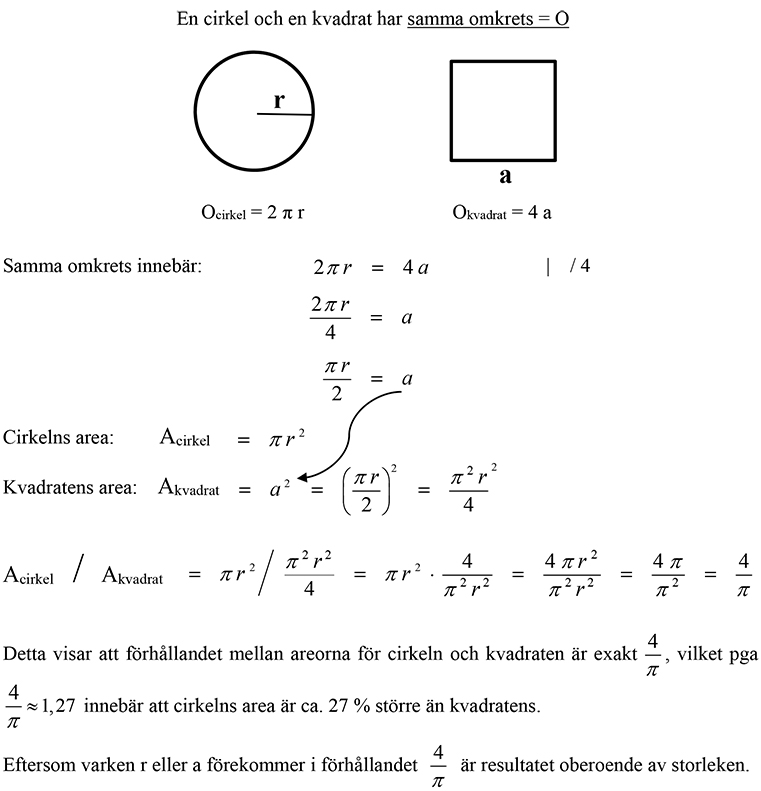
Generell lösning
Steg 3 Lös uppgiften generellt med \( \, r \, \) och \( \, a \, \) som variabler. Ställ upp uttryck för areorna.
Bilda förhållandet (kvoten) mellan figurernas areor dvs \( \, \displaystyle \frac{A_{cirkel}}{A_{kvadrat}} \, \).
Räkna exakt dvs bibehålla \( \, \pi \, \) som bokstav och använd hela tiden bråk istället för decimaltal.
Förenkla kvoten så långt som möjligt. Vilken figur har alltid större area?
Är resultatet beroende av figurernas storlek, dvs av \( \, r \, \) och \( \, a \, \)?
Ange hur många procent den ena figuren är större än den andra.
Copyright © 2024 Lieta AB. All Rights Reserved.