Skillnad mellan versioner av "Primtal"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(12 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
−
__TOC__
+
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
{{Not selected tab|[[Lektion 17 (Inbyggd)| <<&nbsp;&nbsp;Agenda]]}}
 
{{Not selected tab|[[Lektion 17 (Inbyggd)| <<&nbsp;&nbsp;Agenda]]}}
 
<!-- {{Not selected tab|[[Programmering av inbyggda system: Innehåll och struktur|Innehåll & struktur]]}} -->
 
<!-- {{Not selected tab|[[Programmering av inbyggda system: Innehåll och struktur|Innehåll & struktur]]}} -->
−
{{Not selected tab|[[Kryptering|Dagens genomgång]]}}
 
 
{{Selected tab|[[Primtal|Genomgång Primtal]]}}
 
{{Selected tab|[[Primtal|Genomgång Primtal]]}}
−
{{Not selected tab|[[Övningar 17 (Inbyggd)|Dagens övningar]]}}
+
{{Not selected tab|[[Rekursion|Genomgång Rekursion]]}}
−
{{Not selected tab|[[Lektion 18 (Inbyggd)|Nästa lektion&nbsp;&nbsp;>> ]]}}
+
{{Not selected tab|[[Övningar 18 (Inbyggd)|Dagens övningar]]}}
 +
{{Not selected tab|[[Lektion 19 (Inbyggd)|Nästa lektion&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
Rad 66: Rad 66:
 
</div>
 
</div>
  
−
<br>
 
  
−
= <b><span style="color:#931136">Fortsätt med [[Övningar 18 (Inbyggd)|<span style="color:blue">Dagens övningar</span>]].</span></b> =
+
= <b><span style="color:#931136">&nbsp; Genomgång av [[Övningar_18_(Inbyggd)|<span style="color:blue">övn 1901</span>]] och [[Övningar_18_(Inbyggd)|<span style="color:blue">övn 1905</span>]]</span></b> =
 +
<div class="ovnC">
 +
=== <b><span style="color:#931136">Fermat, Euler och de första n primtalen</span></b> ===
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Ovn_1901.jpg]]</div>
  
 +
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Ovn_1905.jpg]]</div>
 +
</div>
 +
 +
 +
= <b><span style="color:#931136">Orientering om primtal</span></b> =
 +
<div class="ovnE">
 +
<big><b><span style="color:red">Vårt mål:</span></b> Ett pythonprogram som delar upp ett givet primtal i primfaktorer: <b>svårt problem!</b>
 +
 +
----
 +
 +
<b><span style="color:red">Tre steg för att uppnå målet:</span></b>
 +
 +
<b>Förra lektion:</b>
 +
 +
<b><span style="color:red">Steg 1</span></b> &nbsp; När är ett tal primtal? Programmet [[1.9 Primtal (Introduktion)#Programmet_PrimtalsTest|<span style="color:blue"><b>PrimtalsTest</b></span>]], modulariserat: [[1.9 Primtal (Introduktion)#PrimtalsTest som funktion|<span style="color:blue"><b>PrimFkt</b></span>]] & [[1.9 Primtal (Introduktion)#Programmet_PrimTest|<span style="color:blue"><b>PrimTest</b></span>]].
 +
 +
----
 +
 +
<b>Idag:</b>
 +
 +
<b><span style="color:red">Steg 2</span></b> &nbsp; Programmet <b>AllaPrimtal</b> hittar alla primtal i ett intervall, använder modulen <b>PrimFkt</b>.
 +
 +
<b><span style="color:red">Steg 3</span></b> &nbsp; Programmet <b>PrimFaktorer</b> faktoriserar ett primtal, modifierar modulen <b>PrimFkt</b>.
 +
</big>
 +
</div>
 +
 +
 +
= <b><span style="color:red">Steg 2</span></b> &nbsp; <b><span style="color:#931136">Alla primtal i ett intervall</span></b> =
 +
<div class="ovnC">
 +
=== <b><span style="color:#931136">Funktionen primtest()</span></b> ===
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: PrimFkt.jpg]]</div>
 +
 +
 +
<big><big>Kan användas som modul i <b>alla</b> program för att avgöra om ett tal är primtal.
 +
 +
Vi använder modulen i programmet nedan för att hitta alla primtal i ett intervall.
 +
</big></big>
 +
</div>
 +
 +
 +
<div class="ovnC">
 +
=== <b><span style="color:#931136">Programmet AllaPrimtal</span></b> ===
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: AllaPrimtal.jpg]]</div>
 +
</div>
 +
 +
 +
= <b><span style="color:red">Steg 3</span></b> &nbsp; <b><span style="color:#931136">Primtalsfaktorisering</span></b> =
 +
<div class="ovnA">
 +
=== <b><span style="color:#931136">Algoritmen Primtalsfaktorisering</span></b> ===
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Algoritmen_Primtalsfaktoriseringa.jpg]]</div>
 +
 +
 +
=== <b><span style="color:#931136">Programmet PrimFaktorer</span></b> ===
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Programmet_Primtalsfaktorisering.jpg]]</div>
 +
</div>
 +
 +
 +
= <b><span style="color:#931136">Fortsätt med [[Övningar 18 (Inbyggd)|<span style="color:blue">Dagens övningar</span>]].</span></b> =
  
  
 
<br>
 
<br>
−
+
 
 +
&nbsp;
 +
 
 +
 
 +
 
  
  

Nuvarande version från 31 januari 2024 kl. 09.57

        <<  Agenda          Genomgång Primtal          Genomgång Rekursion          Dagens övningar          Nästa lektion  >>      


Om primtal

Ord() Om primtal.jpg


Vårt mål:

Ett pythonprogram som åstadkommer faktoriseringen ovan: svårt problem!

Tre steg för att uppnå målet:

Steg 1   När är ett tal primtal? Svar ges av:

  Programmet PrimtalsTest, modulariserat: PrimFkt & PrimTest.

Steg 2   Att hitta alla primtal i ett givet intervall: Programmet AllaPrimtal.

Steg 3   Att faktorisera ett givet primtal: Programmet PrimFaktorer.

Steg 1 tar vi idag, steg 2 & 3 nästa lektion.


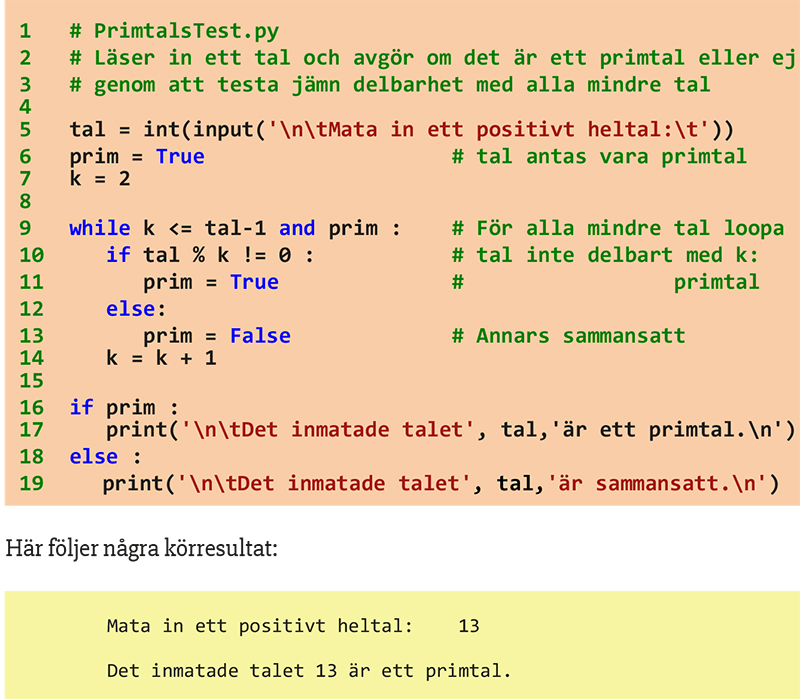
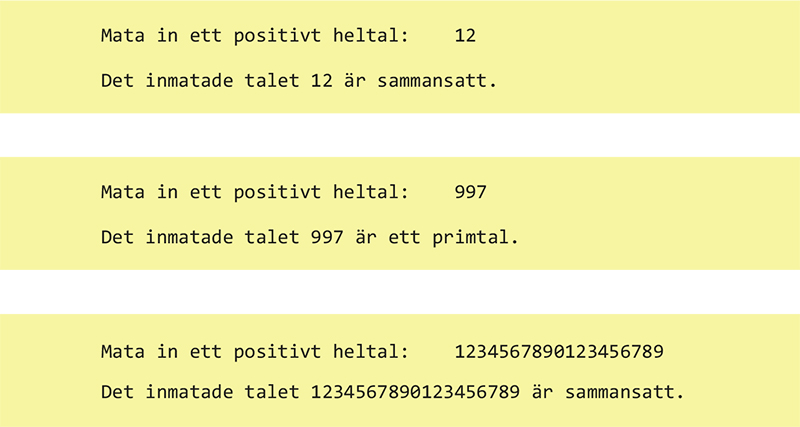
Steg 1   Programmet PrimtalsTest

PrimtalsTest.jpg


PrimtalsTestKorRes.jpg


PrimtalsTest som funktion

Den externa funktionen primtest()

PrimFkt.jpg


Kan användas som modul i alla program för att avgöra om ett tal är primtal.


Programmet PrimTest

Använder modulen ovan och anropar funktionen primtest()

PrimTest.jpg


  Genomgång av övn 1901 och övn 1905

Fermat, Euler och de första n primtalen

Ovn 1901.jpg


Ovn 1905.jpg


Orientering om primtal

Vårt mål: Ett pythonprogram som delar upp ett givet primtal i primfaktorer: svårt problem!

Tre steg för att uppnå målet:

Förra lektion:

Steg 1   När är ett tal primtal? Programmet PrimtalsTest, modulariserat: PrimFkt & PrimTest.

Idag:

Steg 2   Programmet AllaPrimtal hittar alla primtal i ett intervall, använder modulen PrimFkt.

Steg 3   Programmet PrimFaktorer faktoriserar ett primtal, modifierar modulen PrimFkt.


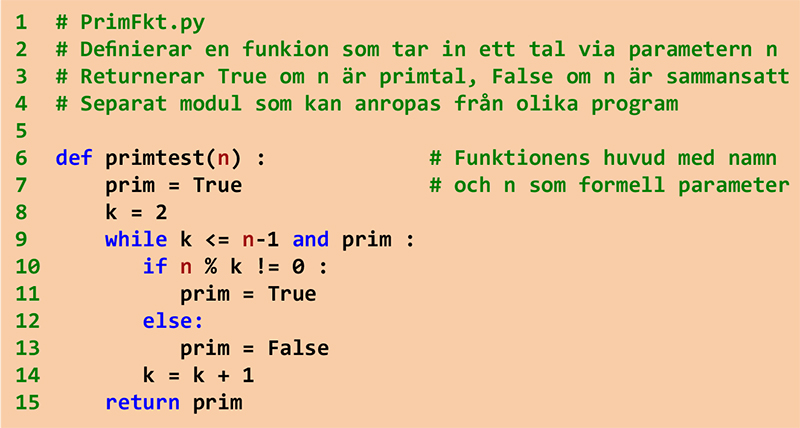
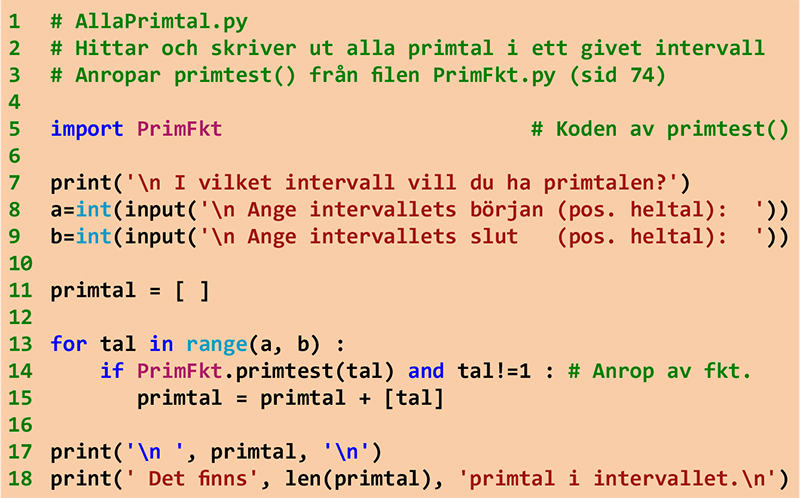
Steg 2   Alla primtal i ett intervall

Funktionen primtest()

PrimFkt.jpg


Kan användas som modul i alla program för att avgöra om ett tal är primtal.

Vi använder modulen i programmet nedan för att hitta alla primtal i ett intervall.


Programmet AllaPrimtal

AllaPrimtal.jpg


Steg 3   Primtalsfaktorisering

Algoritmen Primtalsfaktorisering

Algoritmen Primtalsfaktoriseringa.jpg


Programmet PrimFaktorer

Programmet Primtalsfaktorisering.jpg


Fortsätt med Dagens övningar.


 








Copyright © 2023 TechPages AB. All Rights Reserved.

Hämtad från "https://kurser.mathonline.se/index.php?title=Primtal&oldid=12956"