Skillnad mellan versioner av "Kap 3 Fortsättning med C Cpp (5)"

Från Mathonline
Hoppa till: navigering, sök
m
m
Rad 11: Rad 11:
  
 
<br>
 
<br>
 +
 +
= <b><span style="color:#931136">3.6 &nbsp; Rekursion</span></b> =
 +
<div class="ovnC">
 +
=== <b><span style="color:#931136"> &nbsp; Vad är rekursion?</span></b> ===
 +
<big><big>Ordet <b><span style="color:red">rekursion</span></b> kommer från det latinska <i>recurrere</i> som betyder <b><span style="color:red">att köra igen</span></b>. Dvs:
 +
 +
 +
Man återvänder till något som man redan gjort en gång och <b><span style="color:red">upprepar</span></b> ett känt förlopp,
 +
kanske under andra förutsättningar.
 +
 +
 +
Rekursion är ett koncept som används i problemlösning genom <b><span style="color:red">successiv upprepning</span></b>.
 +
 +
 +
Hittills har vi realiserat upprepning i programmering med loopar. Rekursion är ett alternativ till loopar.
 +
</big></big>
 +
</div>
 +
 +
 +
= <b><span style="color:#931136">Fibonaccis probem</span></b> =
 +
<div class="ovnA">
 +
== <b><span style="color:#931136">Kaniners fortplantning</span></b> ==
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Fibonacciproblemet.jpg]]</div>
 +
 +
 +
<big><big>Följer man Fibonaccis instruktioner för kaniners fortplantning får man följande siffror:</big></big>
 +
 +
== <b><span style="color:#931136">Fibonaccitalen</span></b> ==
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Fibonaccitalen.jpg]]</div>
 +
 +
 +
<table>
 +
<tr>
 +
<td><big><big><b><span style="color:red">Mönster</span></b> för bildningen av Fibonaccis talföljd, <br><br> även kallad <b>Fibonaccitalen:</b></big></big> <br><br> <div class="border-divblue">
 +
<big><b>Summan av två på varandra följande <br> fibonaccital ger nästa fibonaccital.</b></big>
 +
</div>
 +
</td>
 +
<td><math> \qquad\qquad\qquad </math></td>
 +
<td>[https://sv.wikipedia.org/wiki/Leonardo_Fibonacci [[Image: FibonacciBildb.jpg]]]</td> </tr>
 +
</table>
 +
</div>
 +
 +
 +
= <b><span style="color:#931136">Fibonaccis rekursionsformel</span></b> =
 +
<div class="ovnC">
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: FibonacciRekFormel.jpg]]</div>
 +
 +
 +
<big>
 +
Mer utförligt om om Fibonacciproblemet kan du läsa [http://34.248.89.132:1800/index.php?title=1.5_Kontinuerliga_och_diskreta_funktioner#Exempel_3_Fibonaccis_problem <b><span style="color:blue">här</span></b>].
 +
 +
Fibonaccis rekursionsformel kan direkt tas över till följande pythonprogram:
 +
</big>
 +
</div>
 +
 +
 +
= <b><span style="color:#931136">Programmet Fibonacci</span></b> =
 +
<div class="ovnA">
 +
 +
<big>I Python kan Fibonaccis rekursionsformel kodas som en <b><span style="color:red">rekursiv funktion fib()</span></b>.
 +
 +
En funktion kallas för <b><span style="color:red">rekursiv</span></b> om den anropar sig själv i sin egen definition.
 +
</big>
 +
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: FibonacciProgr.jpg]]</div>
 +
 +
<big>Funktionen <b><span style="color:red">fib()</span></b> anropar sig själv två gånger i sin definition på rad 9: <b><span style="color:red">rekursiva anrop!</span></b>
 +
 +
Anropet på rad 14 är ett vanligt (inte rekursivt) funktionsanrop i huvudprogrammet.
 +
</big>
 +
</div>
 +
 +
== <b><span style="color:#931136">Körresultat</span></b> ==
 +
<div class="ovnA">
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: FibonacciKorEx.jpg]]</div>
 +
</div>
 +
  
 
= <b><span style="color:#931136">3.6 &nbsp; Mer om flervägsval</span></b> =
 
= <b><span style="color:#931136">3.6 &nbsp; Mer om flervägsval</span></b> =

Versionen från 7 januari 2024 kl. 15.20

        <<  Agenda          Genomgång 5          Övningar 5          Innehåll & struktur          Nästa lektion  >>      


3.6   Rekursion

  Vad är rekursion?

Ordet rekursion kommer från det latinska recurrere som betyder att köra igen. Dvs:


Man återvänder till något som man redan gjort en gång och upprepar ett känt förlopp, kanske under andra förutsättningar.


Rekursion är ett koncept som används i problemlösning genom successiv upprepning.


Hittills har vi realiserat upprepning i programmering med loopar. Rekursion är ett alternativ till loopar.


Fibonaccis probem

Kaniners fortplantning

Fibonacciproblemet.jpg


Följer man Fibonaccis instruktioner för kaniners fortplantning får man följande siffror:

Fibonaccitalen

Fibonaccitalen.jpg


Mönster för bildningen av Fibonaccis talföljd,

även kallad Fibonaccitalen:

Summan av två på varandra följande
fibonaccital ger nästa fibonaccital.

\( \qquad\qquad\qquad \) FibonacciBildb.jpg


Fibonaccis rekursionsformel

FibonacciRekFormel.jpg


Mer utförligt om om Fibonacciproblemet kan du läsa här.

Fibonaccis rekursionsformel kan direkt tas över till följande pythonprogram:


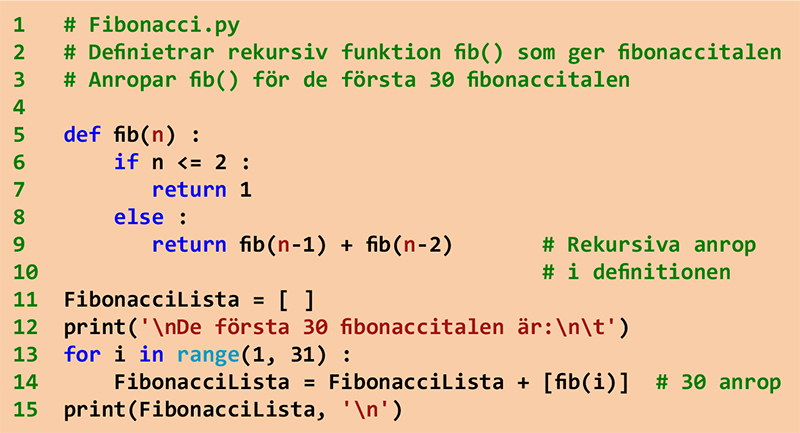
Programmet Fibonacci

I Python kan Fibonaccis rekursionsformel kodas som en rekursiv funktion fib().

En funktion kallas för rekursiv om den anropar sig själv i sin egen definition.

FibonacciProgr.jpg

Funktionen fib() anropar sig själv två gånger i sin definition på rad 9: rekursiva anrop!

Anropet på rad 14 är ett vanligt (inte rekursivt) funktionsanrop i huvudprogrammet.

Körresultat

FibonacciKorEx.jpg


3.6   Mer om flervägsval

Bläddra igenom kursboken:
\( \qquad\;\;\, \)
Luriga else, sid 64.
\( \qquad\;\;\, \)
Kör programmen \( \;\; \)­TrickyElse, sid 64.
och \( \qquad\qquad\quad\;\; \)­NestdIfElse, sid 66.\( \quad \)


switch med tomma case-satser

Bläddra igenom kursboken, sid 67.\( \quad \)
Kör programmet SwitchInequ, sid 67-68.\( \quad \)



Gå vidare till:   
Övningar 5
    när du är klar med denna genomgång.










Copyright © 2024 TechPages AB. All Rights Reserved.

Hämtad från "https://kurser.mathonline.se/index.php?title=Kap_3_Fortsättning_med_C_Cpp_(5)&oldid=12221"