Skillnad mellan versioner av "3.7 Rekursion"
Från Mathonline
Taifun (Diskussion | bidrag) (Skapade sidan med '__NOTOC__ v 49, ht 2022 {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | style="border-bottom:1px solid #797979" width="5px" | {{Not selected...') |
Taifun (Diskussion | bidrag) m |
||
| Rad 12: | Rad 12: | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| + | |||
| + | |||
| + | = <b><span style="color:#931136">Vad är rekursion?</span></b> = | ||
| + | <div class="border-divblue"> | ||
| + | [[Image: Vad_Rekursion.jpg]] | ||
| + | </div> | ||
Versionen från 3 december 2022 kl. 17.16
v 49, ht 2022
| << Agenda | Genomgång Primtal | Genomgång Rekursion | Dagens övningar | Nästa lektion >> |
Vad är rekursion?
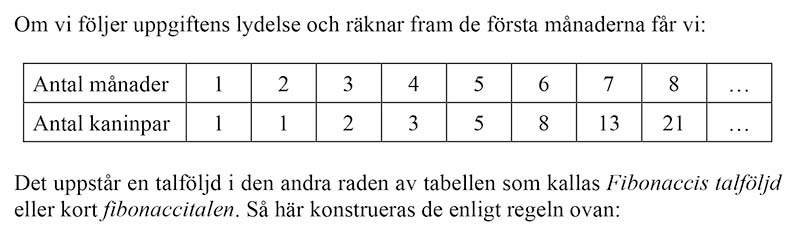
Problemet
Talföljden
Matematisk modell: en rekursionsformel
Regeln: För att få ett fibonaccital addera de två föregående fibonaccitalen.
Rekursionen består i att gå tillbaka (latin: recurrere) och upprepa regeln.
Pga "två föregående" behövs initialt två startvärden \( \; \mathbf{F_1} \, \) och \( \, \mathbf{F_2} \, \).
Rekursionsformeln kallas i matematiken för differensekvation av andra ordningen
som kan lösas explicit, vilket är komplicerat, se Matte 3c.
Vi föredrar programmering med rekursiv metod:
Rekursionsformelns implementation: rekursiva metoden Fib()
Programmet FibonacciTest
Copyright © 2021 TechPages AB. All Rights Reserved.