Skillnad mellan versioner av "4.1 Lathund till Potenser"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m (Taifun flyttade sidan 1.7 Lathund till Potenser Webbversion till 4.1 Lathund till Potenser utan att lämna en omdirigering) |
(Ingen skillnad)
| |
Versionen från 24 juni 2017 kl. 15.33
| Genomgång Potenser | Quiz (Matte 1b) | Övningar (Matte 3c) | Lathund Webb (Matte 1b) | Nästa avsnitt >> |
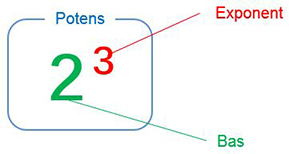
Potens
 |
Potens med positiv exponent: \( \quad\;\;\; 2\,^{\color{Red} 3} \; = \;\; \underbrace{2 \, \cdot \, 2 \, \cdot \, 2}_{{\color{Red} 3}\;\times} \; = \; 8\) Potens = upprepad multiplikation av \( \, 2 \, \) med sig själv, \( \, {\color{Red} 3} \, \) gånger. |
Potens med exponenten \( \, {\color{Red} 0} \, \): \( \qquad\quad \displaystyle 2\,^{\color{Red} 0} \;\; = \;\; 1 \)
|
Potens med negativ exponent: \( \qquad \displaystyle 2\,^{\color{Red} {-3}} \; = \;\; \frac{1}{2\,^{\color{Red} {3}}} \; = \; \frac{1}{8} \quad \) Invertera potensen med positiv \( \quad \) exponent. Att "invertera" t.ex. \( \, 10 \, \) ger \( \, \displaystyle {1 \over 10} \; \). |
Potenslagarna
Första potenslagen: \( \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad \)
Andra potenslagen: \( \qquad\qquad\qquad\;\;\; \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad \)
Tredje potenslagen: \( \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad \)
Lagen om nollte potens: \( \qquad\qquad\quad\;\;\, a\,^0 \; = \; 1 \qquad\qquad \)
Lagen om negativ exponent: \( \qquad\quad\;\;\; a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad \)
Potens av en produkt: \( \qquad\qquad\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad \)
Potens av en kvot: \( \qquad\qquad\qquad\, \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad \)
Grundpotensform
Definition:
\( a \cdot 10\,^n \; \) kallas grundpotensform om \( n \, \) är heltal och \( \; 1 \leq \) \( a \) \( < 10 \; \).
Dvs \( \, a \, \) måste vara mellan \( \, 1,\ldots \, \) och \( \, 9,\ldots \; \).
Copyright © 2010-2017 Math Online Sweden AB. All Rights Reserved.
