Skillnad mellan versioner av "1.1 Räta linjens ekvation i k-form"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 3: | Rad 3: | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{Not selected tab|[[ | + | {{Not selected tab|[[Startsida_Matte_2c| << Startsida]]}} |
{{Selected tab|[[1.1 Räta linjens ekvation i k-form|Genomgång]]}} | {{Selected tab|[[1.1 Räta linjens ekvation i k-form|Genomgång]]}} | ||
{{Not selected tab|[[1.1 Övningar till Räta linjens ekvation i k-form|Övningar]]}} | {{Not selected tab|[[1.1 Övningar till Räta linjens ekvation i k-form|Övningar]]}} | ||
Versionen från 31 mars 2024 kl. 20.44
| << Startsida | Genomgång | Övningar | Innehållsförteckning | Nästa avsnitt >> |
Begreppsförklaring
OBS! Begreppet Ekvation har en annan betydelse här än i algebra.
- Algebra: "Ekvation" = En likhet mellan två uttryck med en obekant, t.ex. 3 + x = 2x.
- Man kan lösa en ekvation som kan ha en eller flera lösningar, ibland ingen alls.
- Här: "Ekvation" = Formeln för en funktion med två variabler, t.ex. y = 4x - 5.
- En funktion y = f(x) beskriver ett samband, ofta ett förlopp (modell av verkligheten).
- Man kan rita en funktions graf för att visualisera förloppet.
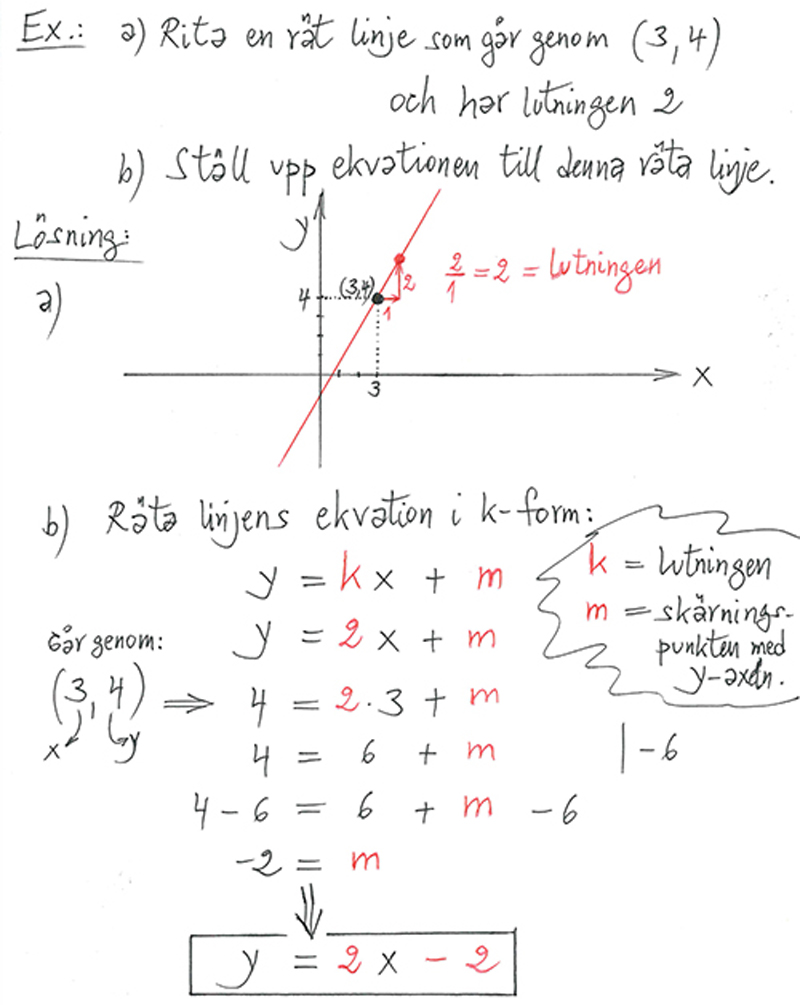
Den räta linjens ekvation är en linjär funktion
Funktionens graf är en rät linje med lutningen k, i exemplet ovan 2.
Därav "k-formen": y = k x + m k kallas även för riktningskoefficient.
k och m är konstanter, medan x och y är variabler.
m är linjens skärningspunkt med y-axeln (när x = 0), i exemplet ovan -2.
Linjens skärningspunkt med x-axeln (när y = 0) kallas för nollställe.
En funktion kallas linjär, om x-termen har icke-neg. exponenter inte högre än 1.
En linjär funktions graf är alltid en rät linje.
Copyright © 2024 Lieta AB. All Rights Reserved.