Skillnad mellan versioner av "4.2 Potenser med rationella exponenter & Potensekvationer"

Från Mathonline
Hoppa till: navigering, sök
(Skapade sidan med ' == <b><span style="color:#931136">Potenser med rationella exponenter</span></b> == <div class="tolv"> <!-- tolv6 --> Potenser med exponenter som är 1.1_Om_tal#Olika_typer...')
 
m
Rad 1: Rad 1:
 +
__NOTOC__
 +
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 +
| style="border-bottom:1px solid #797979" width="5px" | &nbsp;
 +
{{Not selected tab|[[1.1 Polynom| <<&nbsp;&nbsp;Tillbaka till Polynom]]}}
 +
{{Selected tab|[[Potenser|Genomgång]]}}
 +
{{Not selected tab|[[Quiz till Potenser|Quiz (Matte1b)]]}}
 +
{{Not selected tab|[[Övningar till Potenser|Övningar]]}}
 +
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 +
|}
 +
 +
 +
== <b><span style="color:#931136">Hur räknar du?</span></b> ==
 +
<div class="exempel">
 +
[[Image: Hur raknar du Potenser 20.jpg]]
 +
<big>
 +
:<math> {\rm {\color{Red} {OBS!\quad Vanligt\,fel:}}} \quad\; 2\,^3 \; = \; 6 </math>
 +
 +
:<math> \qquad\quad\;\, {\rm Rätt:} \qquad\qquad\! 2\,^3 \; = \; 2 \cdot 2 \cdot 2 \; = \; 4 \cdot 2 \; = \; 8 </math>
 +
</big></div>  <!-- exempel -->
  
  

Versionen från 3 april 2017 kl. 15.37

        <<  Tillbaka till Polynom          Genomgång          Quiz (Matte1b)          Övningar      


Hur räknar du?

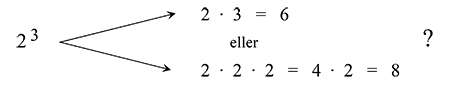Hur raknar du Potenser 20.jpg \[ {\rm {\color{Red} {OBS!\quad Vanligt\,fel:}}} \quad\; 2\,^3 \; = \; 6 \]

\[ \qquad\quad\;\, {\rm Rätt:} \qquad\qquad\! 2\,^3 \; = \; 2 \cdot 2 \cdot 2 \; = \; 4 \cdot 2 \; = \; 8 \]


Potenser med rationella exponenter

Potenser med exponenter som är rationella tal (bråktal) är ett annat sätt att skriva rötter.

Därför kan de användas för att beräkna både kvadratrötter och högre rötter.

Följande samband råder mellan potenser med rationella exponenter och rötter:

Påstående:

Lagen om kvadratroten \( \quad a^{1 \over 2} \; = \; \sqrt{a} \)

Bevis:

Vi multiplicerar \( a \)\(^{1 \over 2} \) två gånger med sig själv och använder första potenslagen:

\( \displaystyle a^{1 \over 2} \cdot a^{1 \over 2} \; = \; a^{{1 \over 2} + {1 \over 2}} \; = \; a^{2 \over 2} \; = \; a^1 \; = \; a \)

Å andra sidan är definitionen för kvadratroten ur \( \, a \):

\( \qquad\quad \displaystyle \sqrt{a} \; = \; \) Tal som 2 gånger multiplicerat med sig själv ger \( \, a \).

Av raderna ovan följer:

\( \displaystyle a^{1 \over 2} \; = \; \sqrt{a} \)


I följande ska alltid gälla: \( \quad m, n \, \) heltal och \( \, n \, \neq 0 \quad \).

Påstående:

Lagen om högre rötter \( \quad a^{1 \over n} \; = \; \sqrt[n]{a} \)

Bevisidé:

Vi visar påståendet för specialfallet \( \, n=3 \):

Vi multiplicerar \( a \)\(^{1 \over 3} \) tre gånger med sig själv och använder första potenslagen:

\( \displaystyle a^{1 \over 3} \cdot a^{1 \over 3} \cdot a^{1 \over 3} \; = \; a^{{1 \over 3} + {1 \over 3} + {1 \over 3}} \; = \; a^{3 \over 3} \; = \; a^1 \; = \; a \)

Å andra sidan är definitionen för 3:e roten ur \( \, a \):

\( \qquad\quad \displaystyle \sqrt[3]{a} \; = \; \) Tal som 3 gånger multiplicerat med sig själv ger \( \, a \).

Av raderna ovan följer:

\( \displaystyle a^{1 \over 3} \; = \; \sqrt[3]{a} \)

Denna bevisidé kan vidareutvecklas till det allmänna fallet:

Lagen om rationell exponent \( \quad \displaystyle a^{m \over n} \; = \; \sqrt[n]{a^m} \)

Tabellen över Potenslagarna borde kompletteras med dessa lagar för rationella exponenter.

Hämtad från "https://kurser.mathonline.se/index.php?title=4.2_Potenser_med_rationella_exponenter_%26_Potensekvationer&oldid=90"