3.8 Parabelns symmetrilinje & extremvärden

<<  Förra avsnitt

Genomgång

Övningar

Nästa avsnitt  >>

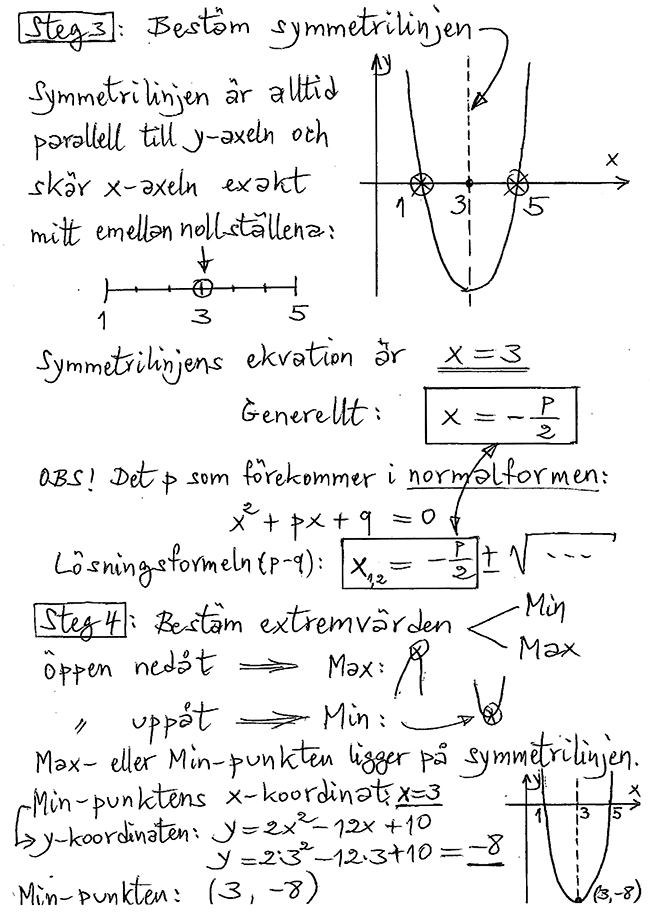
Andragradsfunktion   

Steg 3 & 4

Generellt:

  Symmetrilinjens formel \( \qquad \boxed{\;\; x \; = \; - \, \displaystyle\frac{\color{Red} p}{2} \;\;}\)

  kan användas direkt och bygger på normalformen:

\( \qquad\qquad\qquad x^2 \, + \, \color{Red} p\,x \, + \, q \; = \; 0 \)

  Man behöver inte bestämma nollställena först.

Bevis:

Andragradsfunktionen \( \, y \, = \, x^2 + p\,x + q \,\) har enligt pq-formeln nollställena:\( \quad \displaystyle x_{1,2}=-\frac{p}{2}\pm\sqrt{\bigg(\frac{p}{2}\bigg)^2-q}\)

Symmetrilinjen skär x-axeln exakt mitt emellan nollställena, dvs är deras medelvärde:

\( \displaystyle \frac{x_1 + x_2}{2} \, = \, \left(\left(-\frac{p}{2} \, + \, \sqrt{\bigg(\frac{p}{2}\bigg)^2-q}\right) \, + \, \left(-\frac{p}{2} \, - \, \sqrt{\bigg(\frac{p}{2}\bigg)^2-q}\right)\right) \Big / 2 \, = \, \left(-\frac{p}{2} \, - \, \frac{p}{2}\right) \Big / 2 \, = \, - \, \frac{\color{Red} p}{2}\)

De båda rotuttrycken tar ut varandra när vi löser upp parenteserna. V.s.b.   (Vilket skulle bevisas)

  Extrempunktens x-koordinat: \( \qquad\quad x_{extr} \, = \, - \, \displaystyle\frac{\color{Red} p}{2} \)

  y-koordinaten fås genom att sätta in \( \, x_{extr}\) i andragrads-

  funktionens ursprungliga allmänna form:

\( \qquad\qquad\qquad y_{extr} \; = \; a\,x_{extr}^2 \, + \, b\,x_{extr} \, + \, c \)

Copyright © 2024 Lieta AB. All Rights Reserved.